Построение в Аррениусовских координатах

Суть построения

Просто

Данное построение используется в химической кинетике и выполняется в координатах логарифма константы скорости реакции ($ln(k)$, ось ординат) от обратной температуры ($1/T$, ось абсцисс). Чаще всего используются для анализа влияния температуры на скорость химической реакции. Для реакции первого порядка данное построение имеет вид прямой линии, из которой можно определить энергию активации и предэкспоненциальный множитель.

Наша рабочая группа в статьях и тезисах приводит полное построение и сопутствующее ему описание, если позволяет объём публикации. При сильно сжатом объёме приводится только уравнение для построения линии и полученные результаты.

Сложно

Уравнение Аррениуса может быть записано в форме ур. 1 или ур. 2:

$k = Ae^{\frac{-E_a}{RT}}$ (Ур. 1)

$k = Ae^{\frac{-E_a}{k_BT}}$ (Ур. 2)

Различие между способами записи в единицах измерения энергии. Ур. 1 использует соотношение энергия/моль, типичное для химии, ур. 2 использует непосредственно энергию, что более типично для физики. Учитываются различные единицы при использовании либо газовой постоянной $R$, либо постоянной Больцмана $k_B$.

Ур. 2 может быть расширено до ур. 3:

$ln(k) = ln (A) - \frac{E_a}{R}\Big(\frac{1}{T}\Big)$ (Ур. 3),

где $k$ - константа скорости, $A$ - предэкспоненциальный множитель, $E_a$ - энергия активации, $R$ - универсальная газовая постоянная, $T$ - абсолютная температура, К.

При построении, описанном в разделе “Просто”, значение пересечения графика с осью OY даёт $ln(A)$, а угловой коэффициент прямой будет равен $-E_a/R$. Эти значения могут быть получены путём простой линейной регрессии при помощи электронной таблицы (пример).

Предэкспоненциальный множитель $A$ является эмпирической константой пропорциональности, которая была оценена различными теориями, учитывающими такие факторы, как частота столкновения между реагирующими частицами, их относительная ориентация и энтропия активации.

Выражение $e^{-E_a/RT}$ представляет долю молекул в газе, имеющих энергии, равные или превышающие энергию активации при определенной температуре. Практически во всех случаях $E_a \gg RT$, так что это отношение очень мало и быстро растёт с увеличением $T$. В результате константа скорости реакции $k$ быстро увеличивается с температурой $T$, как показано на прямой линии графика $k(T)$. Чисто математически при очень высоких температурах возможна ситуация, в который $E_a \ll RT$, тогда $k$ должна выровняться и приблизиться к $A$, как к пределу. На практике никогда такого не было.

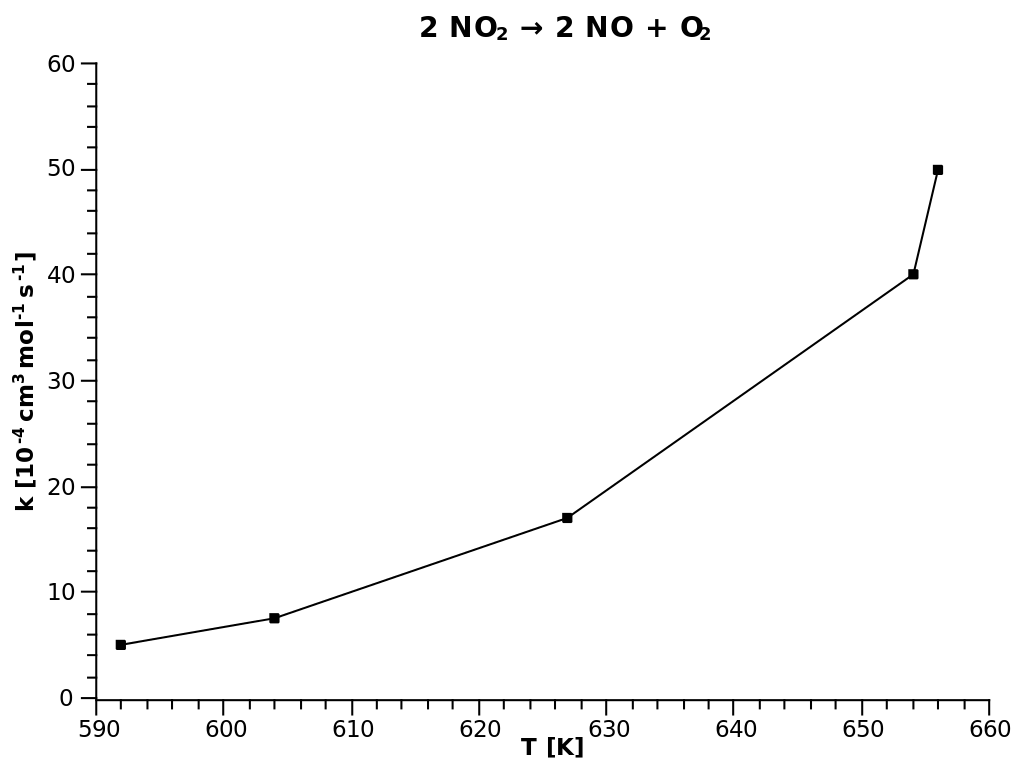
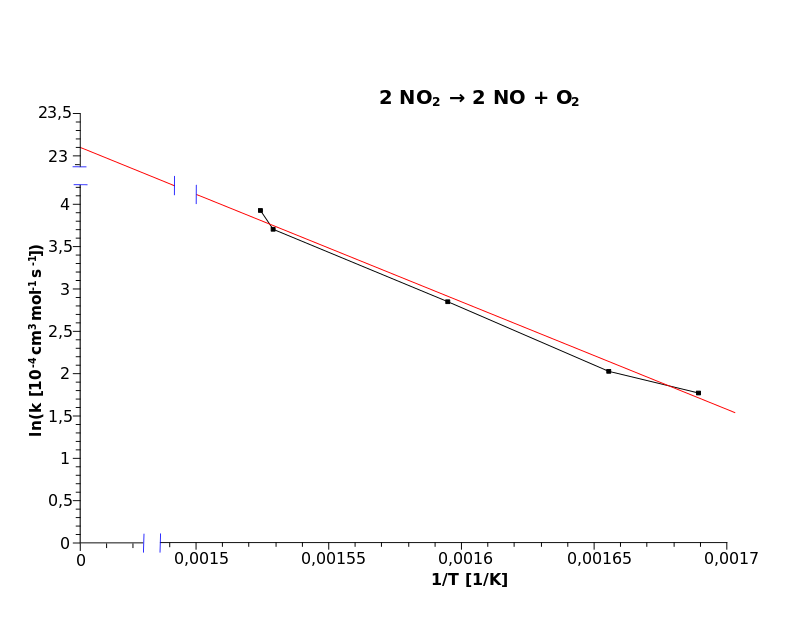
Рис. 1 Прямое построение зависимости $k$ от $T$	Рис. 2 Построение в Аррениусовских координатах: $ln(k)$ от $1/T$

Пример

Обратимся к красной “линии наилучшего соответствия” на рис. 2.
Пусть $y = ln(k[10^{−4} см^3 моль^{−1} с^{−1}])$
Пусть $x = 1/T [K]$

Возьмём с графика следующие точки:
$y = 4,1$ при $x = 0,0015$
$y = 2,2$ при $x = 0,00165$

Угловой коэффициент красной линии будет равен $(4,1 - 2,2) / (0,0015 - 0,00165) = -12,667$

Точка пересечения (значение $y$ при $x = 0$) для красной линии будет равна $4,1 + (0,0015 \cdot 12667) = 23,1$

Подставив данные значения в ур. 3, получим:

$ln(k) = 23,1 - 12,667(1/T)$ (Ур. 4)\
$k = e^{23,1} \cdot e^{-12,667/T}$ (Ур. 5)

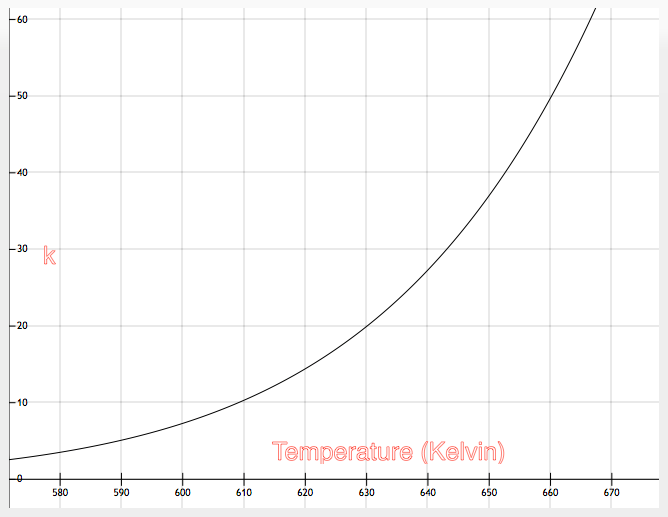
Можно выполнить построение:

Рис. 3: Построение для ур. 5

Отсюда $k = 1,08 \cdot 10^{10} \cdot e^{-12,667/T}$ для $k$ в $10^{-4} \cdot см^3 \cdot моль^{-1} \cdot с^{-1}$ и $T$ в К.

Выполним подстановку в отношение

$-E_a / R = -12,667 K$

которое при приблизительном значении $R = 8,31446$ $Дж \cdot K^{−1} \cdot моль^{−1}$ даст нам энергию активации, полученную из наших данных:

$E_a = R \cdot 12,667 K = 105300$ $Дж \cdot моль^{−1} = 105,3$ $кДж \cdot моль^{−1}$.

Мне кажется, что это довольно просто. Попробуйте и вы!